 |
|
Leçon IV : L'ANALYSE FRÉQUENTIELLE
On peut diviser l'analyse de systèmes linéaires
en deux grandes classes: l'analyse temporelle où l'on observe le
comportement du système en fonction du temps, et l'analyse fréquentielle
où la variable de contrôle est la fréquence. Le but
de cette leçon est d'introduire à cette dernière approche.
Pour les systèmes linéaires, l'analyse fréquentielle permet de connaître la réponse du système à une excitation sinusoïdale, à différentes fréquences. Dans cette leçon, on montre la présentation courante de ces résultats : les diagrammes de Bode. Ces diagrammes peuvent être réalisés expérimentalement ou à partir d'un calcul théorique. On étudie ainsi deux circuits très répandus : les filtres RC passe-haut et passe-bas qui sont les filtres électroniques les plus rudimentaires. ______________________________________________________
PLAN DE LA LEÇON IV
| 1. Analyse fréquentielle
expérimentale 1.1. Définition de l'analyse harmonique expérimentale 1.2. Diagrammes de Bode 1.3. Ordre du système et pente du gain 1.4. Exemple de diagramme de Bode |
2.
Analyse fréquentielle à l'aide des nombres complexes
2.1. Exemple typique : le circuit RC passe-bas 2.2. Exemple typique : circuit RC passe-haut |
| 3.
Remarques générales 3.1. Analyse fréquentielle par Fourier 3.2. Simulation et analogie mécanique 3.3. Remarque : les filtres électroniques |
4. Exercices
/ 5. Corriges
4.1. Lecture d'un diagramme de Bode 4.2. Analyse harmonique de circuits RL 4.3. Circuit RC en situation réelle 4.4. Diagrammes de Bode 4.5. Diagrammes de Bode 4.6. Fonctions de transfert 4.7. Analyse harmonique 4.8. Diagramme de Bode 4.9. Diagramme de Bode 4.10. Analyse harmonique |
_________________________________________________________________ ____________________________________
1. ANALYSE FREQUENTIELLE EXPERIMENTALE
_____________
1.1. Définition
de l'analyse harmonique expérimentale
1.2. Diagrammes de Bode
1.3. Ordre du système
et pente du gain
1.4. Exemple de diagramme
de Bode
1.1. Définition : analyse harmonique expérimentale
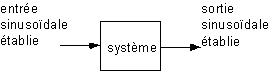
A titre didactique ou réellement expérimental, on peut effectuer une analyse harmonique partielle d'un système. Le principe est le suivant :
- On impose en entrée du système
à étudier une tension sinusoïdale, à une fréquence
fixée.
- On attend un certain temps que le régime
soit stabilisé. On appelle cela le régime sinusoïdal
établi. (Pour plus de détails à ce sujet, voir la
leçon suivante).
|
- On relève le gain en amplitude et le déphasage du système.
- On recommence l'opération pour une large plage de fréquences (ou de pulsation).
Le résultat de ce type de mesure est un ensemble de deux graphes : gain-pulsation et déphasage-pulsation. On parle de diagramme de Bode lorsqu'on en fait une représentation en échelle logarithmique pour les pulsations.
La représentation courante en électronique est donnée sous forme de diagrammes de Bode, où l'on montre l'évolution du gain en décibels et du déphasage en fonction de la pulsation de travail, placée elle aussi en échelle logarithmique.
Exemple de diagramme de Bode en amplitude :
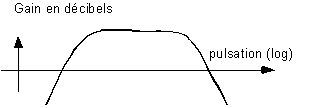
Exemple de diagramme de Bode en phase :
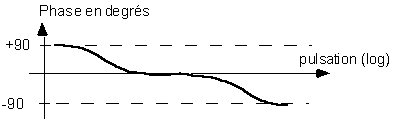
1.3. Ordre du système et pente du gain
On peut reconnaître l'ordre du système à la pente du gain : un système du premier ordre se comporte asymptotiquement avec un affaiblissement de 6 décibels par octave, ou 20 décibels par décade. En général, n fois 6 dB pour un système du nième ordre.
Rappelons qu'une octave correspond à un doublement de fréquence, une décade à une multiplication par dix.
L'expression des pulsations en échelles logarithmiques permet donc de faire apparaître cette propriété qui par ailleurs sert à schématiser des diagrammes de Bode :
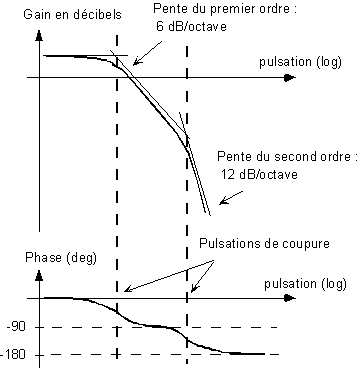
Par exemple, si on considère le diagramme asymptotique suivant :
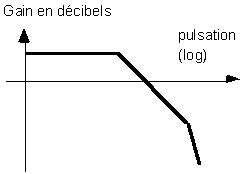
on peut conclure que le système est du second ordre, avec deux pôles simples :
(Cf. Ex. 4.1 : LECTURE D'UN DIAGRAMME DE BODE )
1.4. Exemple de diagramme de Bode
Une analyse harmonique expérimentale permet d'obtenir ce type de diagrammes de Bode : (se référer aux travaux pratiques de laboratoire)
2. ANALYSE FREQUENTIELLE A L'AIDE DES NOMBRES COMPLEXES
_____________
2.1. Exemple typique
: le circuit RC passe-bas
2.2. Exemple typique
: circuit RC passe-haut
Nous avons déjà vu qu'en régime sinusoïdal, on peut représenter les signaux par des vecteurs ou des nombres complexes. Comme l'analyse harmonique d'un système linéaire se fait en régime sinusoïdal établi (voir cours suivant), l'utilisation de nombres complexes (pour l'entrée, la sortie et le gain) est adéquate.
Dans cette approche, le module du gain complexe représente le gain en amplitude et sa phase, le déphasage introduit par le système :
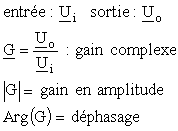
2.1. Exemple typique : le circuit RC passe-bas
Soit le circuit RC suivant, dit "passe-bas" :
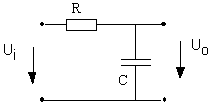
Le gain complexe de ce circuit est donné par :
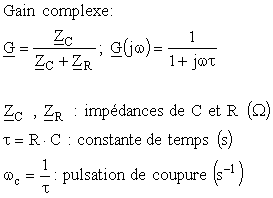
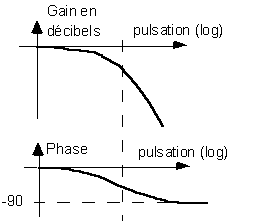
On obtient, pour les diagrammes de Bode :
Le gain en amplitude est déduit du module :
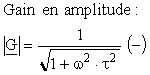
Le déphasage est déduit de l'argument :
2.2. Exemple typique : circuit RC passe-haut
Soit le circuit RC suivant, dit "passe-haut" :
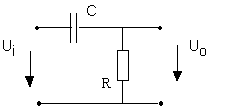
Son gain complexe est donné par :
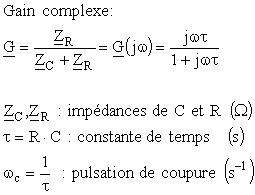
On obtient, pour ses diagrammes de Bode :
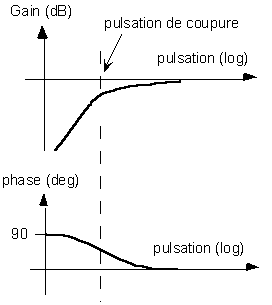
Son gain, déduit du module :
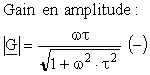
Son déphasage, déduit de l'argument :
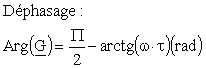
(Cf.
Ex. 4.2 : ANALYSE HARMONIQUE DE CIRCUITS RL
)
(Cf.
Ex. 4.3 : CIRCUIT RC EN SITUATION RÉELLE
)
(Cf.
Ex. 4.4 : DIAGRAMME DE BODE )
(Cf.
Ex. 4.5 : DIAGRAMME DE BODE )
(Cf.
Ex. 4.6 : FONCTIONS DE TRANSFERT )
(Cf.
Ex. 4.7 : ANALYSE HARMONIQUE )
(Cf.
Ex. 4.9 : DIAGRAMME DE BODE )
(Cf.
Ex. 4.10 : ANALYSE HARMONIQUE )
3. REMARQUES GENERALES
_____________
3.1. Analyse fréquentielle
par Fourier
3.2. Simulation et analogie
mécanique
3.3. Remarque : les
filtres électroniques
3.1. Analyse fréquentielle par Fourier
De ce qui précède, on note simplement qu'il est possible de caractériser un système linéaire en régime sinusoïdal par un nombre complexe dépendant de la fréquence : le gain complexe. Ce que nous aborderons dans la leçon consacrée à l'analyse de Fourier, c'est qu'il existe une transformation linéaire, la transformation de Fourier, permettant de caractériser le système linéaire dans des espaces fréquentiels, quel que soit son régime de travail, sinusoïdal ou non. Cette caractérisation est donc aussi valable en particulier pour le régime harmonique. Cette transformation de Fourier permet d'aborder la question du traitement de signal en électronique. (Voir leçon VI)
3.2. Simulation et analogie mécanique
Comme nous savons qu'un circuit électronique RLC par exemple peut représenter un système mécanique, il est aisé de voir qu'il est possible (et cela se faisait il y a quelques années encore) de faire des simulations électroniques de gros systèmes mécaniques comme des turbines, systèmes automatiques, procédés chimiques etc. ... De nos jours, l'ordinateur permet d'effectuer ces opérations numériquement, avec une particulière efficacité pour les systèmes linéaires. Parallèlement, les systèmes électroniques se sont alourdis, et on recourt aussi à des logiciels de conception et simulation pour l'électronique. Dans ces logiciels, il est clair que l'analyse harmonique est une fonction de base. Deux mini-projets sont prévus sur un outil de ce type, un à la fin de chaque semestre (voir le programme du semestre, distribué en classe).
3.3. Remarque : les filtres électroniques
Nous avons déjà évoqué le problème du filtrage. Sous une forme ou sous une autre, ces questions se retrouvent dans toutes les disciplines de l'ingénierie, que ce soit à titre de sous-système à réaliser (par exemple un filtre passe-bande pour les systèmes audio), de systèmes à maîtriser (les questions de vibrations en mécanique par exemple, ou d'immunité au bruit de circuits électroniques) ou de sous-systèmes "parasites" qu'on cherche à connaître (par exemple, la cellule RC modélisant une courte ligne de transmission). En électricité, le filtrage peut être analogique ou informatique. (Voir "Filtres électriques, [23] et "Traitement numérique des signaux", [24])
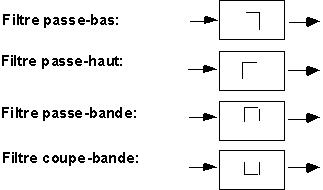
Remarque
Le circuit RLC était utilisé dans les récepteurs radio comme un filtre passe-bande, avec sélection de la fréquence par ajustement de la valeur de la capacité (tuning).
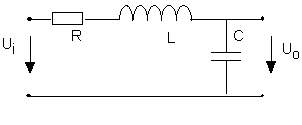
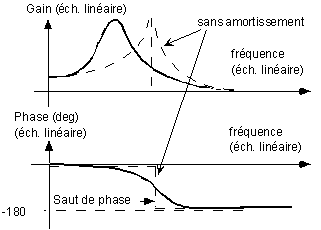
On a les diagrammes de Bode (échelle linéaire) correspondant :
4. EXERCICES
_____________
4.1. Lecture d'un
diagramme de Bode
4.2. Analyse harmonique
de circuits RL
4.3. Circuit RC en situation
réelle
4.4. Diagrammes de Bode
4.5. Diagrammes de Bode
4.6. Fonctions de transfert
4.7. Analyse harmonique
4.8. Diagramme de Bode
4.9. Analyse harmonique
4.1.
Lecture d'un diagramme de Bode
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Soit le diagramme en amplitude, provenant d'une analyse expérimentale :
On postule un système du second ordre, avec deux pôles simples :
- Placez 
sur le diagramme ci-dessus.
On introduit dans le système correspondant au diagramme expérimental précèdent, un signal carré de 20 Khz.
- Est-il réaliste de s'attendre à
un affaiblissement de 50 % de l'amplitude de la première harmonique
(composante à 40KHz), par rapport à la fondamentale (composante
à 20 KHz) ? (On lit sur le relevé : 
)
4.2. Analyse harmonique de
circuits RL
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Représentez et analysez harmoniquement les circuits RL passe-haut et passe-bas.
4.3.
Circuit RC en situation réelle
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Un circuit RC passe-bas est inséré dans un système qu'on modélise par une source affine et une charge résistive. L'ensemble donne le schéma suivant :
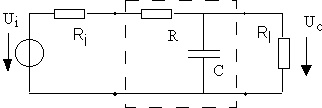
La résistance 
sert à modéliser la résistance de sortie de la source
de tension. La résistance 
est la résistance de charge du circuit ; elle pourrait par exemple
servir à modéliser l'effet de charge de l'oscilloscope d'observation.
La cellule "RC" pourrait modéliser une courte ligne de
transmission, en négligeant les effets inductifs.
- Exprimez sa constante de temps et son gain statique.
- Effectuez une analyse harmonique du quadripôle global, incluant charge et source.
- Quelles sont les conditions sur les valeurs pour qu'on puisse se ramener à la cellule RC de base, en négligeant charge et source ?
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Tracer le diagramme de Bode (en amplitude) de la fonction de transfert suivante :
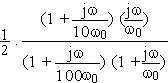
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
a) Factoriser la fonction de transfert suivante:
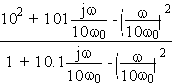
b) Tracer le diagramme de Bode (en amplitude)
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Déterminer les fonctions de transfert correspondant aux diagrammes de Bode suivants :
a)
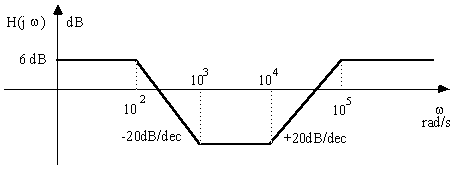
b)
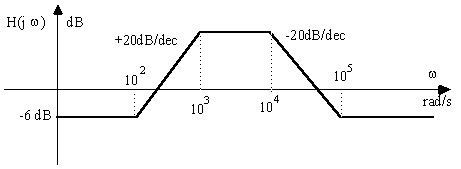
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
On propose le circuit ci-dessous :
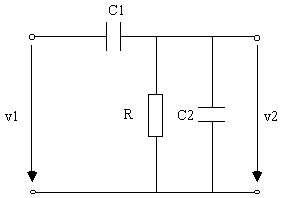
C1 = 100nF C2 = 900 nF R = 1 KW
a) Calculer la fonction de transfert H(jw) = v2/v1
b) Tracer les diagrammes de Bode en amplitude et en phase
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
Représenter dans un diagramme de Bode l'amplitude et la phase de la fonction de transfert H(jw) = pour les deux circuits suivants :
a) b)
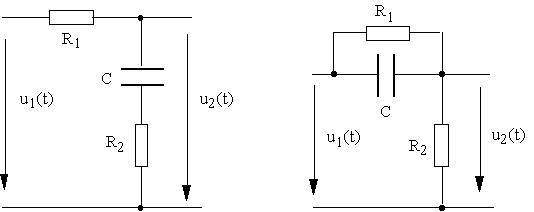
avec dans les deux cas R1 = 999·R2 .
Indiquer la valeur analytique de l'amplitude, de la phase et de la pulsation aux points de brisure.
ÉNONCÉ---Corrigé---Retour au paragraphe correspondant du cours
On donne le circuit suivant avec une source de tension continue V1 et une source de tension alternative v2(t) sinusoïdale.
 |
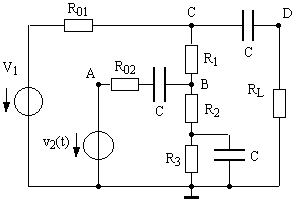V1 = 10 V
v2 = 2sin(wt) [V] R01 = R02 = 50 W R1 = 3 kW R2 = 2 kW R3 = 2 kW RL = 100 kW |
1) Etablir le schéma équivalent en continu et déterminer la composante continue du potentiel aux nœuds A, B, C et D.
2) Etablir le schéma équivalent en alternatif à des fréquences assez hautes pour que les capacités puissent être remplacées par des courts-circuits. Déterminer la composante alternative du potentiel aux nœuds A, B, C et D.
5. CORRIGÉS
_____________
Ex. 4.1. Lecture
d'un diagramme de Bode
Ex. 4.2. Analyse harmonique
de circuits RL
Ex. 4.3. Circuit RC
en situation réelle
Ex. 4.4. Diagrammes
de Bode
Ex. 4.5. Diagrammes
de Bode
Ex. 4.6. Fonctions de
transfert
Ex. 4.7. Analyse harmonique
Ex. 4.8. Diagramme de
Bode
Ex. 4.9. Analyse harmonique
Exercice 4.1. Lecture d'un diagramme
de Bode
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
Soit le diagramme en amplitude, provenant d'une analyse expérimentale:
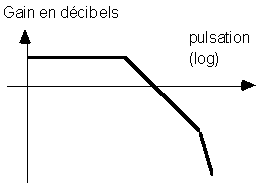
On postule un système du second ordre, avec deux pôles simples :
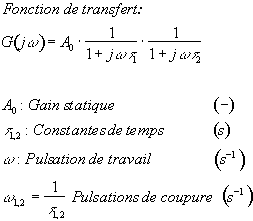
- Placez 
sur le diagramme ci-dessus.
On introduit dans le système correspondant au diagramme expérimental précèdent, un signal carré de 20 kHz .
- Est-il réaliste de s'attendre à
un affaiblissement de 50 % de l'amplitude de la première harmonique
(composante à 40KHz), par rapport à la fondamentale (composante
à 20 kHz) ? (on lit sur le relevé : 
)
| Harmonique | fréquence | pulsation |
| 1 | 20kHz | 125600 s-1 >> w 2 |
| 2 | 40kHz | 251200 s-1 >> w 2 |
La fondamentale et la 1ère harmonique se trouvent dans la région à -40dB par décade de pente.
On a donc : 
La première harmonique est affaiblie de 75% par rapport à la fondamentale.
Exercice 4.2 : Analyse
harmonique de circuits RL
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
Circuit RL passe-haut :
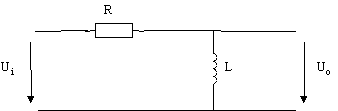
avec : 
Circuit RL passe-bas :
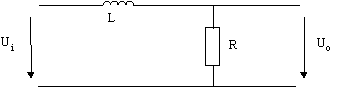
avec :
L’analyse des 2 fonctions de transfert est identique à celles effectuées au point 2 de la leçon IV.
Exercice 4.3 : Circuit
RC en situation réelle
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
Un circuit RC passe-bas est inséré dans un système qu'on modélise par une source affine et une charge résistive. L'ensemble donne le shéma suivant:
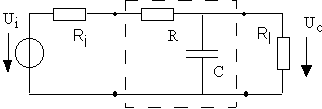
Fonction de transfert : 
avec : 
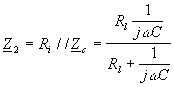
que l’on peut représenter, après mise en forme :
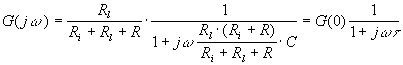
On identifie : 
gain du quadripôle à f=0
constante de temps du système
L’analyse harmonique est celle d’un circuit de 1er ordre standard (voir les travaux pratiques TP3)
Il suffit que : Ri = 0 Pour que ces 2 résistances n’influencent pas le comportement
Rl = ¥ de la cellule RC.
Exercice
4.4 : Diagrammes de Bode
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
Tracer le diagramme de Bode (en amplitude) de la fonction de transfert suivante:
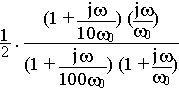
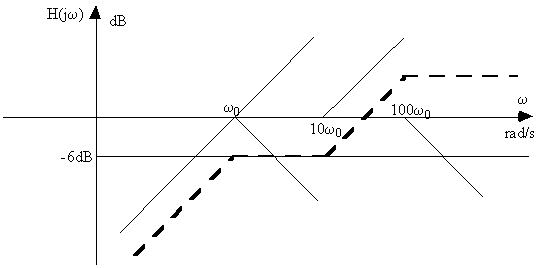
Exercice
4.5 : Diagrammes de Bode
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
a) Factoriser la fonction de transfert suivante:
= 
=
=
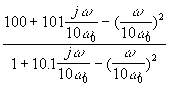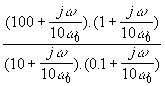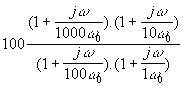
b) Tracer le diagramme de Bode (en amplitude)
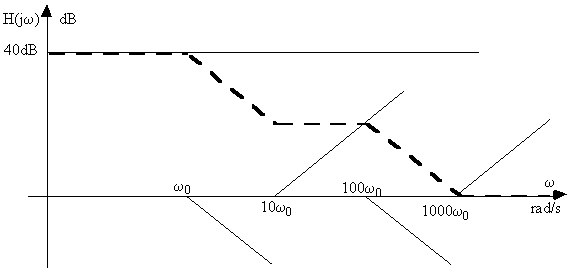
Exercice
4.6 : Fonctions de transfert
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
Déterminer les fonctions de transfert correspondant aux diagrammes de Bode suivants:
a)
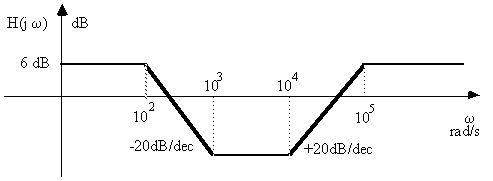
b)
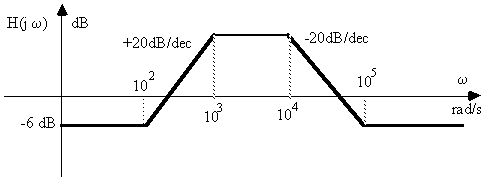
a) H1(jw)
=
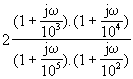
b) H2(jw) = 1/H1(jw)
Exercice
4.7 : Analyse Harmonique
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
On propose le circuit ci-dessous :
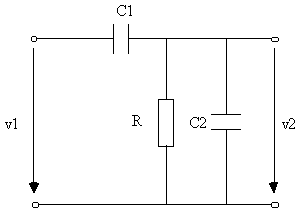
C1 = 100nF C2 = 900 nF R = 1k
a) Calcul de la fonction de transfert H(jw) = v2/v1
Après simplification on trouve H(jw)
= 
w2 = 1/RC1 = 104 rad/s et w1 = 1/R(C1+ C2) = 103 rad/s
Diagrammes de Bode en amplitude et en phase
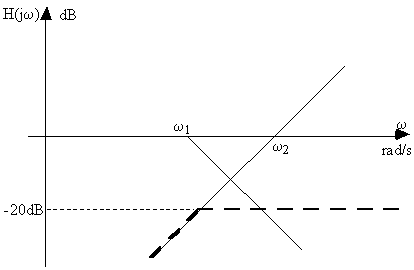
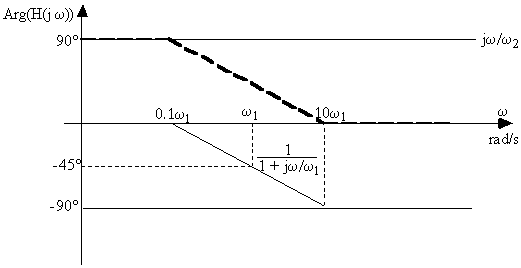
Exercice 4.8 : Diagramme de Bode
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
L’expression de la fonction de transfert du circuit a) est :
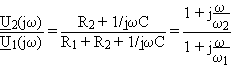
avec w1
= 
w2 =
=
1000w1
(pôle) (zéro)
Le diagramme de Bode est le suivant:
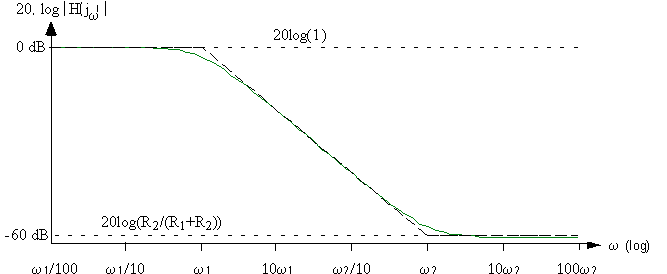
L’expression de la fonction de transfert du circuit b) est :
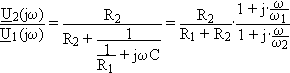
avec w1
=
w2
= 
= 1000w1
(pôle) (zéro)
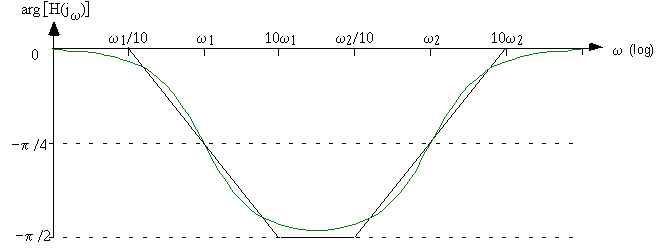
Le diagramme de Bode est le suivant:
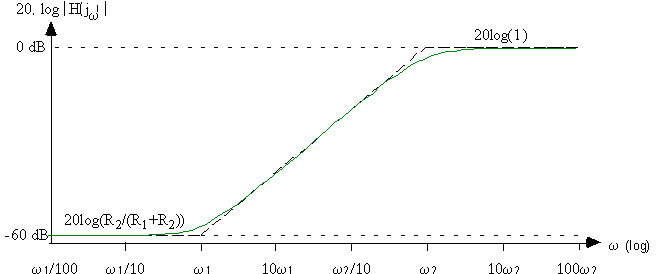
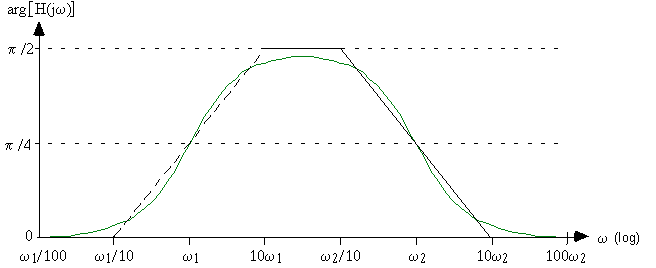
Exercice 4.9 : Analyse Harmonique
CORRIGÉ---Énoncé---Retour au paragraphe correspondant du cours
1) Composante continue.
Pour établir le schéma équivalent en continu: on remplace les capacités par des circuits ouverts. De plus, la composante continue de v2 étant nulle cette source est remplacée par un court-circuit.
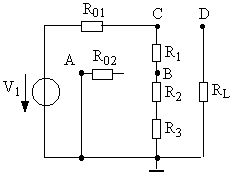
2) Composante alternative.
Pour établir le schéma équivalent pour les signaux alternatifs on remplace les capacités et les sources de tension continues par des courts-circuits.
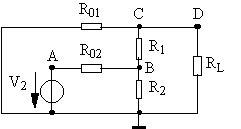
vBeff = 1.36 Veff
vCeff = 22.3 mVeff
_________________________________________________________________
FIN DE LA LECON Numéro IV