Ce cours est destiné à tous ceux qui désirent acquérir les connaissances nécessaires à la compréhension du fonctionnement qualitatif des boucles à verrouillage de phase, mais son but principal est de permettre la conception de montages répondant à des besoins particuliers.
Deux applications seront proposées à titre d'exemples de synthèse : le calcul d'un démodulateur FM et le calcul d'un multiplicateur de fréquence. Ces exemples permettront de comparer les caractéristiques théoriques prévues à celles de montages réels sur lesquels des mesures seront effectuées.
La simple utilisation des formules indiquées sur les feuilles de caractéristiques des boucles à verrouillage de phase n'est pas suffisante. Lors de l'étude d'un système, le concepteur est amené à effectuer des choix de paramètres selon la propriété du système qu'il veut optimiser et une bonne compréhension des phénomènes mis en jeu est indispensable. C'est pourquoi les expressions mathématiques permettant le calcul des différents composants seront à chaque fois justifiées.
La présentation adoptée consiste à partir de systèmes simplifiés. La compréhension en est facilitée, mais des défauts sont mis en évidence. L'élimination progressive de ces défauts permet d'aboutir aux systèmes complets réellement utilisés.
Des notions préalables d'électronique générale et sur les asservissements sont très utiles. Pour fixer les idées, on peut dire qu'un niveau de 1ère année de B.T.S. électronique, d'école d'ingénieur ou de faculté de sciences fondamentales ou technologiques devrait permettre d'atteindre l'objectif.
Tout d'abord, le nom peut en donner une idée. PLL est l'abréviation de Phase Locked Loop, en français boucle à verrouillage de phase.
Le terme boucle provient du domaine des asservissements. Nous sommes donc en présence d'un système asservi appelé aussi en boucle fermée.
Quelle est la grandeur asservie ? Le nom nous l'indique encore, il s'agit de la phase du signal de sortie qui est verrouillée sur la phase du signal d'entrée...
Hum, hum, ça commence déjà à se compliquer ! Ça promet !
Mais non, puisque les choses ne paraissent compliquées que tant qu'on ne les a pas comprises...
L'internaute familier avec la représentation des signaux sous forme de vecteurs tournants, dite représentation de Fresnel, verra tout de suite une conséquence de cet asservissement de la phase du signal de sortie sur celle du signal d'entrée : la fréquence du signal de sortie est forcément elle aussi verrouillée sur celle du signal d'entrée. Tout devrait s'éclaircir lors de l'étude d'un démodulateur FM.
Mais concrètement, sous quelle forme se présente une PLL ? C'est un circuit intégré qui peut être placé dans un boîtier quelconque, par exemple DIP16 ou CMS, et auquel il suffit de connecter quelques composants pour le faire fonctionner.
La naissance de la PLL remonte à 1932, alors qu'un ingénieur nommé DE BELLESCIZE cherchait à améliorer la réception des signaux radioélectriques en modulation d'amplitude. Auparavant, la démodulation de ces signaux se faisait grâce à une détection d'enveloppe obtenue en utilisant un détecteur de crête (circuit comportant une diode, un condensateur et une résistance).
L'inconvénient du détecteur de crête, c'est qu'il est très sensible aux bruits parasites, qu'ils soient d'origine atmosphérique (orages) ou industrielle (moteurs). Les signaux utiles trop faibles étaient donc noyés dans du bruit et devenaient inutilisables.
Un nouveau principe de démodulation, appelé démodulation synchrone, a alors été mis au point. Il nécessite la production, au niveau du récepteur, d'un signal dont la phase est verrouillée sur celle de la porteuse de l'émission reçue. En 1932, à l'époque des tubes, les réalisations à base de PLL étaient volumineuses et chères. C'est pourquoi ce principe a été réservé aux matériels professionnels jusqu'à la généralisation des circuits intégrés.
L'arrivée des circuits intégrés a bouleversé
toutes les branches de l'électronique :
Outre la démodulation synchrone, les différentes applications
possibles de la PLL sont peut-être aussi nombreuses et variées
que celles que l'on a trouvées pour l'amplificateur opérationnel.
On peut citer, sans que cette liste soit limitative :
La structure minimale comprend :
La technologie des PLL peut être analogique (c'est souvent le cas pour les fréquences les plus élevées en R.F.) ou digitale (pour les fréquences moins élevées : jusqu'à 1 à 20 MHz environ selon le type de circuit intégré). Le raisonnement et les équations restent semblables avec les deux technologies.
Afin de ne pas trop effrayer le brave internaute qui lit ces lignes, nous allons commencer en raisonnant sur un schéma facile à comprendre mais qui comporte quelques inexactitudes sur lesquelles nous reviendrons par la suite.
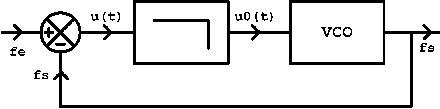
Le comparateur de phase délivre un signal u(t) constitué d'une valeur moyenne uo(t) et de toute une série d'harmoniques. Dans le cas d'une PLL digitale, u(t) est un signal carré positif variant entre 0V et la tension d'alimentation positive. Il est important de retenir que uo(t) est une tension continue proportionnelle au déphasage qui existe entre les deux signaux appliqués sur les entrées du comparateur de phase. Le filtre passe-bas transmet la tension continue uo(t) à l'entrée du VCO qui délivre sur sa sortie une fréquence proportionnelle à uo(t).
Pour simplifier, on va supposer pour l'instant que la fréquence appliquée à l'entrée est constante.
Lorsque la boucle est verrouillée (on dit aussi accrochée), la fréquence fs est exactement égale à la fréquence fe et est donc elle aussi constante.
Puisque fs = cte, uo(t) est une tension continue proportionnelle au déphasage entre ve et vs. Ce déphasage est tel que la valeur moyenne du signal délivré par le comparateur de phase provoque l'oscillation du VCO à fs = fe. Dans ces conditions, les différentes grandeurs sont en régime permanent et ne peuvent évoluer.
En effet, si le déphasage
a tendance à augmenter pour une raison quelconque, la tension uo(t)
va diminuer, entraînant une diminution de fs et donc une diminution
de
qui va s'opposer
à l'augmentation initiale.
Conclusion :
est verrouillé à une valeur qui dépend de fe.
Ce mode de fonctionnement sera étudié plus tard expérimentalement. Il est possible de se reporter directement au paragraphe correspondant en cliquant sur l'oscilloscope ci-dessous (qui fonctionne, mais avec un problème de synchro...) :
La structure minimale peut être complétée par :
On obtient ainsi le schéma fonctionnel simplifié complet suivant :
La fonction de transfert de chacun des blocs du schéma fonctionnel ci-dessus est définie comme suit :
k0 s'appelle la sensibilité du VCO.
![]() .
.
Cette manipulation constitue une étape essentielle pour une bonne compréhension du fonctionnement des PLL. Il est donc indispensable d'effectuer ces travaux pratiques avant de poursuivre l'étude du cours, en cliquant sur l'oscilloscope ci-dessous :
a) Rappels sur les systèmes asservis.
Schéma-bloc d'un système bouclé :
H0(p) : fonction de transfert de la chaîne
directe.
B(p) : fonction de transfert de la chaîne de
retour.
H0(p).B(p) : fonction de transfert
de la boucle fermée.
Fonction de transfert de la boucle fermée :
Formule
de BLACK
Tout schéma-bloc avec une chaîne de retour quelconque peut être transformé, par déplacement de blocs, en un schéma-bloc à retour unitaire.
Lorsqu'un système est à retour unitaire, sa fonction de transfert en boucle fermée devient :
Remarque : lors de la transformation du schéma-bloc, l'expression de H0(p) est modifiée.
b) Schéma fonctionnel définitif.
Le comparateur de phase délivre une tension proportionnelle au déphasage entre les deux signaux d'entrée. Ce sont donc deux phases qui doivent apparaître sur ses deux entrées.
Avec un signal de la forme v = V sin(t)
= V sin(
t +
0)
^
^
^
Phase
instantanée Pulsation Phase
à l'origine
La pulsation est la dérivée par rapport au temps de la phase instantanée :
Réciproquement :
En pratique, les grandeurs d'entrée et de sortie sont des fréquences.
En multipliant une fréquence par 2,
on obtient une pulsation et en multipliant une pulsation par 1/p, on obtient
une phase instantanée. Ces deux multiplications vont faire apparaître
deux nouveaux blocs représentant ces opérations mathématiques
mais qui ne correspondent pas à des éléments matériels.
On peut simplifier ce schéma en déplaçant les blocs
2 et 1/p.
On aboutit ainsi au schéma définitif d'une PLL :
c) Fonction de transfert de la chaîne directe.
On l'obtient en faisant le produit des fonctions de transfert de chaque bloc :
d) Fonction de transfert de la boucle fermée.
Exemple : Application à la PLL étudiée expérimentalement.
Av = 1 (pas d'amplificateur de tension)
kr = 1 (pas de diviseur en retour)
a été
calculé lors de l'étude expérimentale :
Filtre passe-bas RC :
On obtient :
C'est la fonction de transfert classique d'un système du second ordre.
Par identification :
e) Etude de la stabilité de la boucle dans le cas d'un filtre RC.
Expressions littérales de 0
et m :
Choix de m :
Choix de la structure du filtre :
L'étude précédente a été effectuée en prenant pour filtre passe-bas un réseau RC. C'est la solution la plus simple, mais pas la plus performante. De meilleurs résultats peuvent être obtenus facilement en utilisant un filtre passe-bas comportant deux résistances et un condensateur. Cette solution est assez courante (et constitue une source presque inépuisable de sujets de devoirs surveillés...). Par contre, l'usage de filtres actifs d'un ordre plus élevé est rare.
Application numérique :
On choisit m = 0,5, ce qui donnera un dépassement de 16,3 %.
Calculer , la
pulsation propre de la boucle
0
et la fréquence propre de la boucle f0.
Attention : f0 ne représente pas ici la fréquence centrale du VCO.
Une remarque pour terminer : les variations de fontes qui peuvent être observées dans certains passages ne sont pas dues au navigateur mais aux différentes méthodes utilisées (parfois très laborieuses...) pour générer le texte HTML et le texte associé aux formules mathématiques ou aux schémas. Ces problèmes devraient disparaître à l'avenir avec l'apparition de nouvelles normes HTML comprenant la saisie directe des formules.