Equations paramétriques

Le but de ce cours est de montrer les différentes formes de représentation d'une fonction.

Utilisons le cercle pour étudier les différentes formes de représentation graphique.
L’équation d’un cercle centré sur l’origine et de rayon 2 est de la forme
$x^2$ + $y^2$ = 4
Il s’agit d’une fonction de 2 variables f(x,y)

Equation cartésienne

L’équation cartésienne de la forme y = f(x)
donne deux équations :
y = + $\sqrt{4-x^2}$ et
y = - $\sqrt{4-x^2}$

$\mathrm{Plot}\left[\sqrt{4-x^2},\left\{x,-2,2\right\},\mathrm{AspectRatio}\to \mathrm{Automatic}\right]$

$\mathrm{Plot}\left[-\sqrt{4-x^2},\left\{x,-2,2\right\},\mathrm{AspectRatio}\to \mathrm{Automatic}\right]$

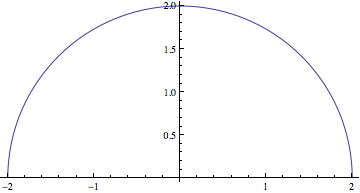
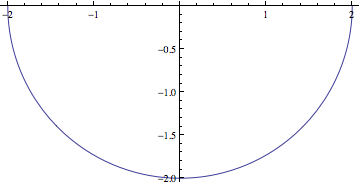
La fonction ContourPlot du logiciel Mathematica trace le contour d’une fonction de deux variables

$\mathrm{ContourPlot}\left[x^2+y^2,\left\{x,-2,2\right\},\left\{y,-2,2\right\},\mathrm{ContourStyle}\to \mathrm{Black},\mathrm{ContourLabels}\to \mathrm{True},\mathrm{ColorFunction}\to \mathrm{Hue}\right]$

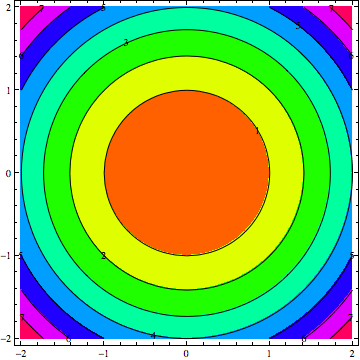
En ajoutant une contrainte telle que $x^2$ + $y^2$ = 4, nous obtenons le cercle de rayon 2

$\mathrm{ContourPlot}\left[x^2+y^2⩵4,\left\{x,-2,2\right\},\left\{y,-2,2\right\}\right]$

Fonction de deux variables

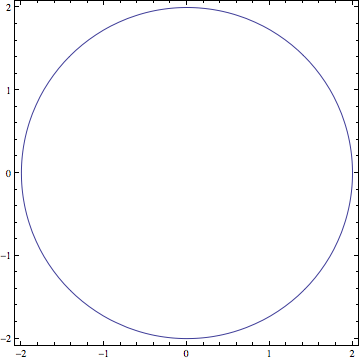
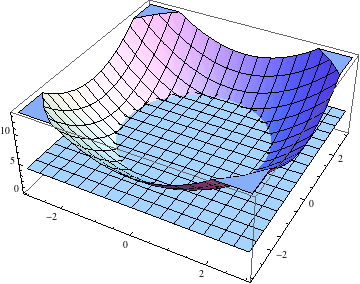
Si nous raisonnons en 3 dimensions, nous pouvons générer un tracé en 3 dimensions d’une fonction de deux variables z = f(x,y)
L’intersection de la fonction z = $x^2$ + $y^2$ avec la fonction z = 4 donne le cercle de rayon 2

$\mathrm{Plot3D}\left[\left\{x^2+y^2,4\right\},\left\{x,-3,3\right\},\left\{y,-3,3\right\}\right]$

Equation paramétrique

En introduisant une nouvelle variable t que l’on nomme paramètre, on peut créer x et y en tant que fonction de t
x(t) = 2 Cos(t)
y(t) = 2 Sin(t)
Nous obtenons l’équation du cercle ${x\left(t\right)}^2$ + ${y\left(t\right)}^2$ = 4
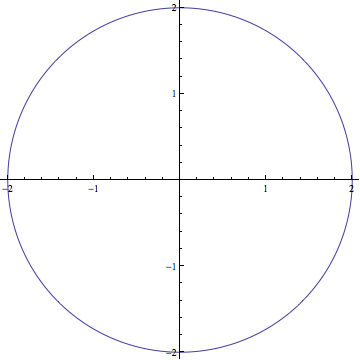
La fonction ParametrcPlot de Mathematica permet de tracer directement les deux fonctions x(t) et y(t)
Ce tracé se nomme équation paramétrique. La valeur du paramètre t est indépendante de la valeur des variables x et y.
Par exemple t varie entre 0 et 2 π, alors que x et y varient entre -2 et 2.

$\mathrm{ParametricPlot}\left[\left\{2\mathrm{Cos}\left[t\right],2\mathrm{Sin}\left[t\right]\right\},\left\{t,0,2\pi \right\}\right]$