Les vecteurs

Les vecteurs sont des nombres 2. Ils sont extrêmement utilisés en Physique.

Représentation des vecteurs

On peut représenter les vecteurs de deux manières différentes :

- soit avec des flèches sur les lettres ou chiffres

 ou  ou

- soit par leur coordonnées dans un repère (O,x,y,z)

 =

Les vecteurs comme des flèches

Une première approche décrit les vecteurs comme des flèches avec 4 caractéristiques :
- le point d'applicaton (qui n'a pas d'influence pour distinguer deux vecteurs égaux avec des points d'application différents)
- la longueur ou module
- la direction
- le sens (pour une direction donnée, il existe deux sens possibles)

Les vecteurs comme des nombres 2

Une seconde approche les étudient come des nombres avec 3 lois spécifiques.

1 - somme de deux vecteurs

La somme vectorielle de deux nombres 2 n'est pas identque à la somme de deux nombres 1.

La somme du [vecteur AB de module 4 ] + [vecteur AC de module 3] donne le [vecteur AD de module 5]

Notons que la soustraction vectorielle n'existe pas

 -  =  + (-)

D'autre part, le théorème de Chasles permet de relier les vecteurs comme un petit train relierai les wagons entre eux.

 +  +  =

2- le produit scalaire

Le produit signifie multiplication et scalaire nombre 1. Cela signifie que cette loi qui relie deux nombres 2 donne comme résultat un nombre 1. On dit que le résutat sort du corps (système de nulérotation avec des lois).

 .  =  x  x  = C

 est un nombre 1,  est un nombre 1,  est un nombre 1 compris entre -1 et +1. Leur multiplication est donc un nombre 1.

Représentation par les coordonnées

 =  ,  = ,     .  = XaXb + YaYb + ZaZb

Notons que deux vecteurs perpendiculaires donnent un produit scalaire nul.

3 - le produit vectoriel

Le résultat d'un produit scalaire est un vecteur. Il reste dans le corps.

Représentation par les flèches

 .  =  x  x  x =

 est un nombre 1,  est un nombre 1,  est un nombre 1 compris entre -1 et +1. Leur multiplication est donc un nombre 1 qui n'est pas un vecteur, il faut donc multiplier par un vecteur  pour obtenir un vecteur .

Les caractéristiques du vecteur  sont les suivantes :

-       son module unitaire est égal à 1

-       sa direction est normale (perpendiculaire) au plan formé par les vecteurs  et

-       son sens est donné par la règle des trois doigts

Représentation par les coordonnées

 =  ,  = ,     ∧  =

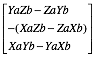
Notons que deux vecteurs colinéaires donnent un produit vectoriel nul.