Mathématiques

En mécanique les translations et les rotations sont les deux mouvements de base.
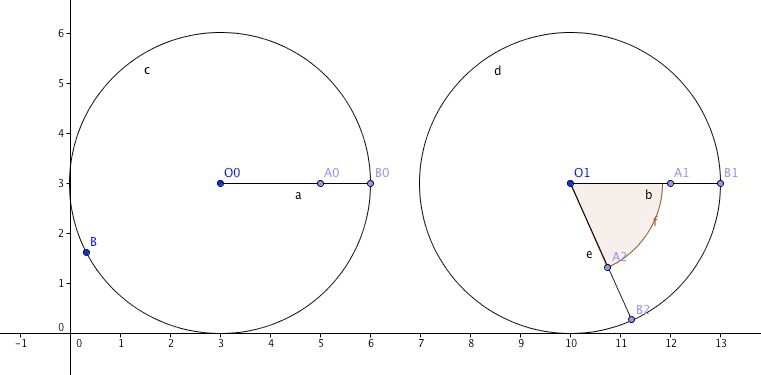
Prenons comme exemple une roue de vélo qui roule de la gauche vers la droite entre les instants t0 et t1.
Le point A passe de A1 à A2 et le point B de B1 à B2.
La longueur de l'arc ![]() est inférieure à
la longueur de l'arc
est inférieure à
la longueur de l'arc ![]() .
.
Ces longueurs ont été parcourues dans le même
temps.
Donc VA < VB [1]
Si nous raisonnons sur l'angle parcouru :
l'angle [A1 O1 A2] est identique à l'angle [B1 O1 B2]
Au lieu d'avoir une vitesse linéaire comme une
![]()
on peut prendre une vitesse angulaire comme un
![]() que nous
noterons ω
que nous
noterons ω
Donc ωA = ωB [2] qui à l'air d'être en contradiction avec l'équation [1]
Il existe une relation de base entre vitesse linaire et vitesse angulaire :
V = ω R (R est la distance entre le centre et le point considéré)
Faisons une comparaisons pour la mécanique des solides entre le linéaire et l'angulaire.

La vitesse est une dérivée de la distance par
rapport au temps ![]()
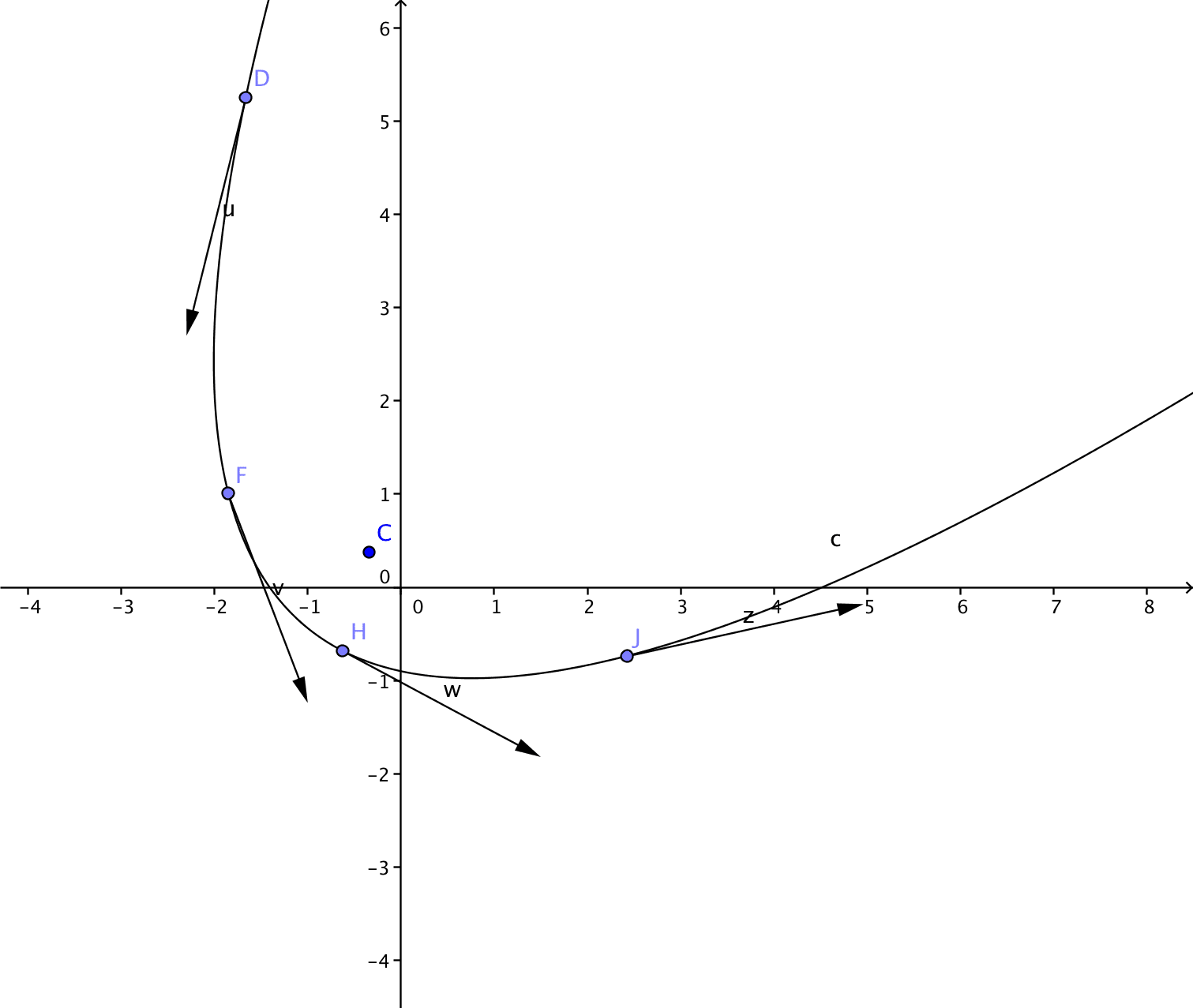
Or la dérivée d'une fonction en un point correspond à la pente de la droite tangente en ce point.
Le vecteur vitesse est tangent à la trajectoire.
Même si Flash est utilisé sur de nombreux sites web, il ne s'agit pas d'une norme internationale et donc, en tant que tel, il ne fait pas partie du Web. En effet, bien qu'un plugin Flash soit préinstallé sur la majorité des ordinateurs grand public, de nombreusystèmes d'exploitations libres ou non, ne disposent pas d'un lecteur. En l'occurrence, GNU/Linux ne dispose d'un plugin que pour processeurs anciens, alors que Linux est disponible sur de nombreuses autres architectures. Bien qu'Adobe ait publié les spécifications partielles de Flash (hors codecs vidéo, par exemple), il n'existe pas d'application de référence, et il est donc impossible de l'utiliser « quelle que soit sa plate-forme ». De plus, l'intégration aux navigateurs par un plugin pose de nombreux problèmes d'accessibilité.
Sur son site, Adobe présente Flash comme « partie des outils pour le Web », mais c'est techniquement faux.
Ce tutoriel offre une solution alternative pour installer Flash sous Android.